相变普适类在自然界和实验体系中广泛存在,并被视为现代临界理论的支柱。在常规的物理图像中,热力学标度和有限尺寸标度均呈现幂律依赖行为。在若干情形下,对数标度被视为幂律行为的修正,统计物理学家Peter Grassberger教授曾用“notoriously difficult”来描述处理此类问题的难度。在前期工作中,我校金沙集团1862cc吕建平教授与中国科学技术大学邓友金教授、新泽西州立罗格斯大学陈锟博士等开展合作,给出上临界维度O(n)模型关联函数和自由能的精确对数有限尺寸标度【National Science Review 8, nwaa212 (2021)】。
近期,吕建平教授课题组与邓友金教授针对O(2)模型的非凡表面相变开展深入研究,致力于探索该相变的新奇对数标度行为。该团队借助于大规模蒙特卡洛模拟,系统验证了强表面耦合O(2)矢量模型中对数临界指数的普适性和标度关系,由此证实对数普适类的存在性。在此基础上,该团队提出基于两距离标度的物理图像:关联函数体现两种对数标度行为的共存,即依赖于距离的行为和依赖于系统尺寸的行为,分别主导短程和长程区间,两种标度由不同的临界指数刻画。该研究结果已在《物理评论快报》(Physical Review Letters)发表,我校19级硕士研究生胡明辉同学是论文的第一作者【Physical Review Letters 127, 120603 (2021)】。
通过上述研究工作,该团队凝练出精确物理图像和大规模数值模拟(模型空间和参数空间)相结合的技术路线,从而为新奇相变现象的研究和后续工作的开展提供借鉴。
我校是上述两篇论文的第一署名单位。相关研究工作受到国家自然科学基金委、国家重点研发计划、上海市科委和安徽省教育厅的资助。

图1 论文信息
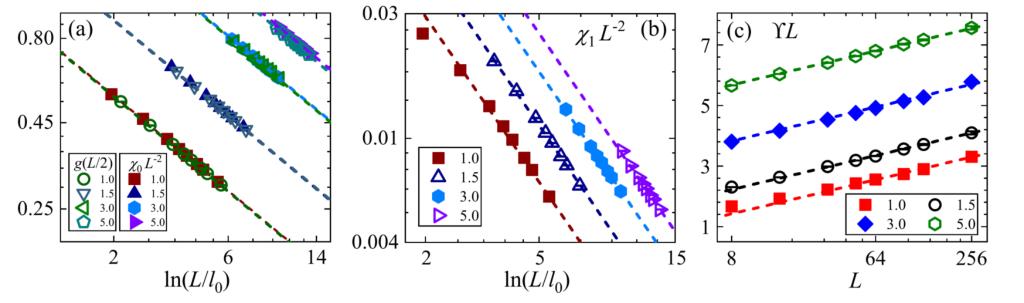
图2 两点关联、磁涨落和螺旋模量的对数标度[PRL 127, 120603 (2021)]
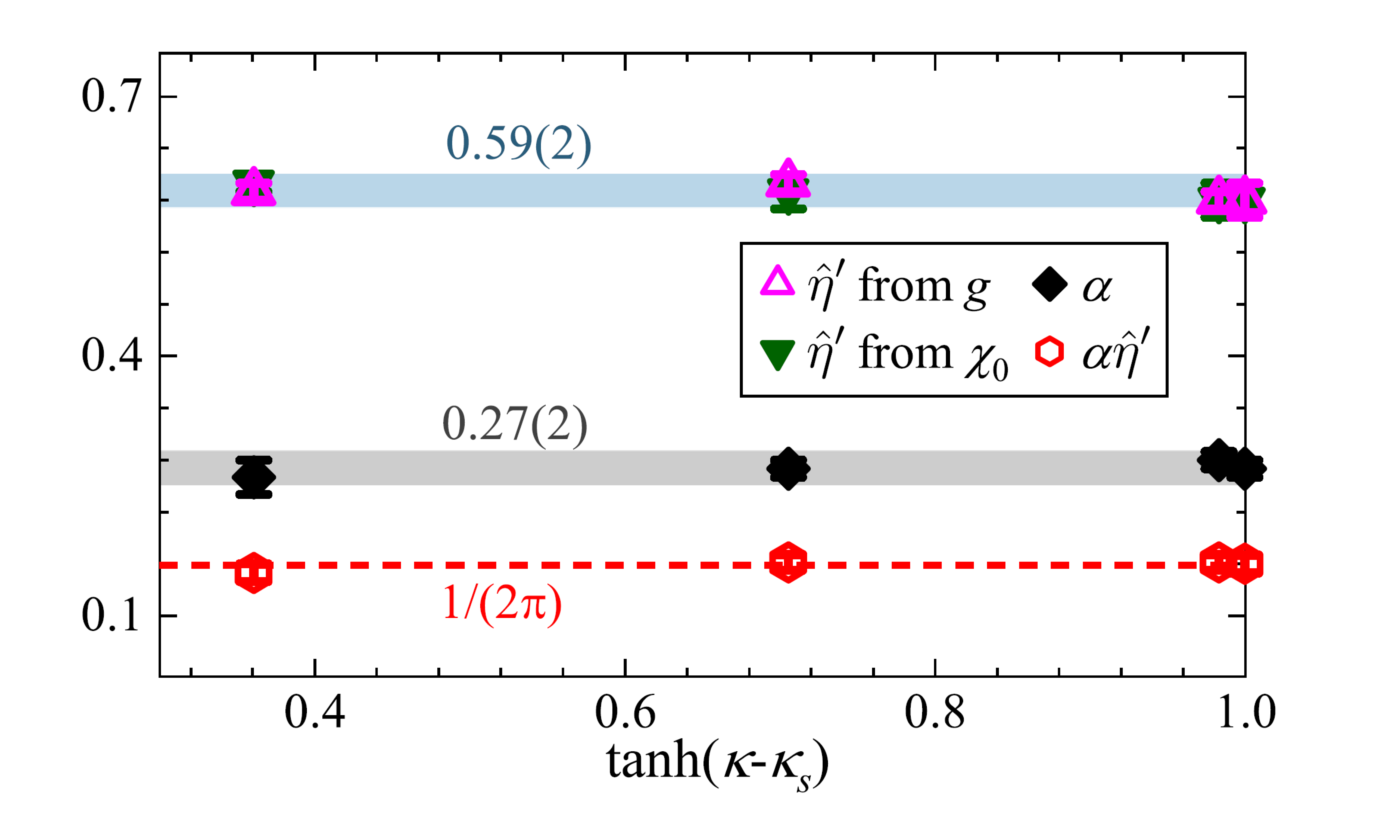
图3 临界指数的普适性和标度关系[PRL 127, 120603 (2021)]
论文链接:https://link.aps.org/doi/10.1103/PhysRevLett.127.120603
https://academic.oup.com/nsr/article/8/3/nwaa212/5899772

